CでDevquiz２０１１スライドパズル その２

解説1

昨日公開したスライドパズルのソースの解説をしていこうと思います。
まずは特に独自性がありそうな、端優先、ステップ実行と書いたアルゴリズムの解説です。

端優先

１	２	３
４	５	６
７	８	０

このような３X３のブロックなしの問題が与えられた場合、人力で解く際は通常、まず１をそろえて、その次２、３、その次４、７、最後に５、６、８と合わせますよね。

このロジックを実装したアルゴリズムです。

ここで２、３を一緒に合わせるのは２を先に合わせて固定してしまうと３が入らなくなるからですが、これは「ある駒（この場合２の駒）を固定することで1方向にしか移動できなくなる駒（この場合は３の駒）を一緒に合わせる必要がある」という考えで一般化でき、具体的には

recurs_func(　駒A　）{
 駒Aを固定する
 for　(　駒B　∈　Aと隣り合っている駒で1方向にしか動かせない駒　）
　　recurs_func(　駒B　）
}

といった再帰で実現できます。

このロジックはブロックがある場合にも拡張でき、例えば

１	２	３	４
５	６	＝	８
９	A	B	C
D	E	F	０

といったケースにもうまく適応できます。

この場合

{1}
{2,3,4,8}
{5,6}
{9,D}
{AE}
{BCF}

といった形の配列を作成し、上から順番にIDA*を利用して揃えていくという事を行っています。

なお、上からそろえる、左からそろえる、左上（０から遠いところから）揃えると3パターンで試してみましたが、これら３つはほぼ等価で、上からそろえてうまくいくものは、左からでも左上からでもうまくいくし、ダメなものはだめという結果でした。

この理由はダメな場合はこの例の｛2,3,4,8}のように一緒に揃えないといけない駒の数が多いとき、IDA*では現実的な計算量に収まらないという状況のようです。
ここは、マンハッタンディスタンス（MD)に加え並び順も考慮することで改善の余地がありそうだったので時間があればもうちょっと開発したかった部分です。

ステップ実行

一般に、駒の移動回数Nが増えるに従いx^Nのオーダーで計算量が増えていきます。

ここで、xは与えられた問題に依存する1から3の間の実数です。（3より小さいのは上下左右4つの方向のうち1方向は前回の盤面に戻る移動なので省略しているから）移動回数とMDの輪が閾値以下という条件で枝刈りするにしてもNが増えると（閾値が増えると）計算量はどうしても膨大になります。

そこで最短経路解を取りこぼしてでも（移動回数の制限はかなりあまいという事がわかっていたので）強めの枝刈りを考える事になるのですが、ここではたとえば1億ノードとか指定してあげて、そのノード数探索して見つからなかったら、それまでに探索したノード内で最もMDの小さい値を初期ノードとして再探索するという事を行いました。つまり、最小値を持つモード以外すべて枝刈りするという大胆な方法です。

双方向探索と同じようにx^Nをx^(N/2)としてあげようという発想ですね。

この方法のメリットはなんといっても実装が簡単である事。

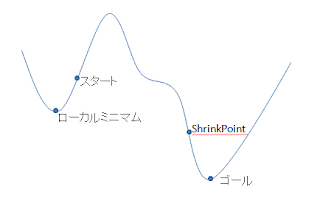
また、ステップ毎に強めの枝刈りをして深く探索していく方法だとローカルミニマムにとらわれて脱出できないリスクが高くなりますが、この方法だと無駄だと思われるノードに対しても与えられた探索回数までは広く探索を行うので、ローカルミニマムから脱出する可能性が高くなるというメリットもあります。

実際、この方法は強力で単純なIDA*では見つけられなかった問題（計算に時間がかかりすぎた問題）のかなりの数を回答しています。

これらのアルゴリズムの位置づけに関してはこちらの記事を参照してください。